Rumus Deret Aritmatika : Barisan, Bentuk, Contoh Soal Dan Jawaban – Barisan bilangan adalah
himpunan bilangan yang diurutkan menurut suatu aturan/pola tertentu
yang dihubungkan dengan tanda “,”. Jika pada barisan tanda “,” diganti
dengan tanda “+”, maka disebut deret.. Masing-masing bilangan itu disebut suku-suku barisan
U1, U2, U3, ….Un
a, a+ b, a+2b, a + 3b, …., a + (n-1) b
Selisih (beda) dinyatakan dengan b
Un = suku ke n dengan n = 1,2,3, …
a = suku pertama → U1 = a
b = selisih/beda




Perhatikan bahwa selisih di antara suku-sukunya selalu tetap. Barisan yang demikian itu disebut barisan aritmetika. Selisih itu disebut beda suku atau beda saja dan dilambangkan dengan c.
Barisan (l) mempunyai beda, b = 4. Barisan ini disebut barisan aritmetika naik karena nilai suku-sukunya makin besar.
Barisan (2) mempunyai beda, b = -5. Barisan ini disebut barisan aritmetika turun karena nilai suku-sukunya makin kecil.
Suatu barisan U1, U2, U3,….disebut barisan aritmetika jika selisih dua suku yang berurutan adalah tetap. Nilai Untuk menentukan suku ke-n dari barisan aritmetika. perhatikan kembali contoh barisan (l).
Secara umum, jika suku pertama (U1) = a dan beda suku yang berurutan adalah b maka dari rumus Un = 3 + 4(n – 1) diperoleh 3 adalah a dan 4 adalah b. Oleh sebab itu, suku ke-n dapat dirumuskan
Un = a + b(n-1)
Barisan aritmetika yang mempunyai beda positif disebut barisan aritmetika naik, sedangkan jika bedanya negatif disebut barisan aritmetika turun.
U1, U2, U3, …….Un-1, Un disebut barisan aritmatika, jika
U2 – U1 = U3 – U2 = …. = Un – Un-1 = konstanta
Un = a + (n-1)b = bn + (a-b) → Fungsi linier dalam n
Jawab:
Diketahui barisan aritmetika 3, 8, 13, …
a + (a + b) + (a+2b) + (a+3b) + … + (a+(n-1)b )
Jumlah suku hingga suku ke n pada barisan aritmatika dirumuskan dengan:
Sn = (2a + (n-1) b ) atau Sn = ( a + Un )
Seperti telah dibahas sebelumnya, deret adalah bentuk penjumlahan dari suku-suku pada sebuah barisan. Jika U1, U2, U3, … barisan aritmetika. U1, U2, U3, … adalah deret aritmetika.
Untuk mendapatkan jumlah n suku pertama dari deret aritmetika, perhatikan kembali deret yang dihasilkan barisan (l ).
3 +7 + 1l + 15 + 19 + …
Jika jumlah n suku pertama dinotasikan dengan.Sn maka S dari deret di atas adalah :
Perhatikan jumlah 5 suku pertama, S yang diperoleh. Angka 3 pada perhitungan tersebut berasal dari suku pertama, sedangkan l9 adalah suku ke-5. Oleh karena itu, jumlah suku ke-n adalah

Beda barisan aritmatika setelah disispkan k buah suku akan berubah dan dirumuskan:

Keterangan:
Penyelesaian:
Diketahui: deret aritmatika mula-mula: 20 + 116
Contoh Soal Deret Aritmatika
Suatu deret aritmatika 5, 15, 25, 35, …
Berapakah jumlah 10 suku pertama dari deret aritmatika tersebut?
Jawab:
b). -250
c). -75
d). -115
c). -250
Penyelesaian :
2. Jumlah 10 suku pertama dari deret aritmatika : 3 + 5 + 7 + 9 + ….. adalah …..
a). 105
b). 120
c). 150
d). 155
e). 165
Penyelesaian :
b). 3
c). 8
d). 10
e). 12
Penyelesaian :
b). 6
c). 9
d). 10
e). 18
b). 44
c). 49
d). -40
e). -44
Penyelesaian :
a + 7b = 23
-4b = -12
b = = 3
Substansi a + 3b = 11
a + 3 (3) = 11
a + 9 = 11
a = 11 – 9 = 2
b). 26
c). 28
d). 31
e). 34
Penyelesaian :
b). 73
c). 77
d). 81
e). 83
Penyelesaian :
b). Rp. 1.255.000
c). Rp. 260.000.000
d). Rp. 1.530.000
Penyelesaian :
b). 875.000 unit
c). 1.125.000 unit
d). 1.375.000 unit
e). 1.625.000 unit
Penyelesaian :
b). 25
c). 26
d). 27
e). 28
Penyelesaian :
b).1950
c).1900
d).1875
e).1825
Penyelesaian :
b).Rp. 340.000
c).Rp. 335.000
d).Rp. 220.000
e).Rp. 700.000
Penyelesaian :
b).8
c).1
d).4
Penyelesaian :
b).-52
c).-46
d).46
e).81
Penyelesaian :
b).8
c).12
d).14
e).16
Penyelesaian :
Contoh 2.1
Penyelesaian:
ke n dari barisan itu dapat diturunkan dengan cara berikut.
pertama a dan beda b adalah:
Diketahui barisan aritmatika dengan unsur ke 2 adalah 10 dan beda = 2.
Tentukan unsur ke 7 barisan itu.
Penyelesaian:
Diketahui U2 = 10, b = 2. Dengan menggunakan rumus Un = a + (n-1)b,
diperoleh
Contoh 2.3
Mulai tahun 2000, Pak Arman mempunyai kebun tebu. Penghasilan kebun
tebu Pak Arman pada akhir tahun 2000 adalah Rp 6.000.000,-. Mulai tahun
2001, Pak Arman memupuk kebun tebunya dengan pupuk kandang. Pak
Arman memperkirakan bahwa setiap akhir tahun, penghasilan kebun tebunya
naik Rp 500.000,-. Berapa perkiraan penghasilan kebun tebu Pak Arman pada
akhir tahun 2005?
Penyelesaian:
Misalkan:
a = penghasilan kebun tebu Pak Arman pada akhir tahun 2000.
b = perkiraan kenaikan penghasilan kebun tebu Pak Arman setiap akhir tahun.
P2005 = perkiraan penghasilan kebun Pak Arman pada akhir tahu 2005.
Jadi a = Rp 6.000.000,-, b = Rp 500.000,-, dan P2005 akan dicari.
Karena perkiraan kenaikan penghasilan kebun tebu Pak Arman setiap
akhir tahun adalah tetap, maka untuk menentukan penghasilan kebun Pak
Arman pada akhir tahun 2005, kita dapat menerapkan rumus unsur ke n dari
barisan aritmatika dengan
adalah Rp 8.500.000,-
Dengan adanya deret aritmatika, kita dapat membentuk barisan yang
terkait dengan deret tersebut. Barisan demikian disebut barisan aritmatika.
Contoh 2.4
Tentukan jumlah 25 suku pertama deret 3 + 6 + 9 +….
Penyelesaian:
Deret 3 + 6 + 9 +…. adalah deret aritmatika dengan a = 3 dan b = 3. Oleh
karena itu dengan menggunakan rumus Sn =
Contoh 2.5
Tentukan jumlah semua bilangan ganjil antara 50 dan 100.
Penyelesaian:
Diketahui a = 51, b = 2, dan Un = 99.
Untuk mencari jumlah semua bilangan ganjil di antara 50 dan 100, pertamatama
kita cari dulu banyaknya bilangan ganjil di antara 50 dan 100, yaitu n
dengan menggunakan rumus:
Pengertian Aritmatika
Aritmatika atau aritmetika yang kata yang berasal dari bahasa Yunani αριθμός = angka yang dulu biasa disebut Ilmu Hitung merupakan cabang tertua (atau pendahulu) dari matematika yang mempelajari operasi dasar bilangan.Barisan Aritmatika
Barisan Aritmetika adalah suatu barisan bilangan dengan pola tertentu berupa penjumlahan yang memiliki beda atau selisih yang sama/tetap.Rumusan Barisan Aritmatika
Suku-sukunya dinyatakan dengan rumus berikut :U1, U2, U3, ….Un
a, a+ b, a+2b, a + 3b, …., a + (n-1) b
Selisih (beda) dinyatakan dengan b
b = U2 – U1 = U3 – U2 = Un – Un – 1Suku ke n barisan aritmatika (Un) dinyatakan dengan rumus:
Un = a + (n-1) bKeterangan :
Un = suku ke n dengan n = 1,2,3, …
a = suku pertama → U1 = a
b = selisih/beda
(1) 3, 7, 11, 15, 19, …
(2) 30, 25, 20, 15, 10,…
Bentuk Barisan Aritmatika
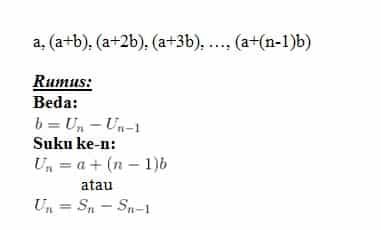
Keterangan:
a = U1 = Suku pertama
b = beda
n = banyak suku
Un= Suku ke-n
Contoh Barisan Aritmatika
- Suku pertama dari barisan aritmatika adalah 3 dan bedanya = 4, suku ke-10 dari barisan aritmatika tersebut adalah …
Penyelesaian:
a = 3
b = 4
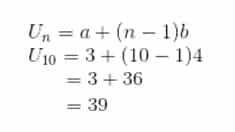
- Diketahui barisan aritmatika sebagai berikut: 5, 8, 11, …
Tentukan: Nilai suku ke-15 !
Penyelesaian:

Suku Tengah Barisan Aritmatika
Jika barisan aritmatika mempunyai banyak suku (n) ganjil, dengan suku pertama a, dan suku terakhir Un maka suku tengah Ut dari barisan tersebut adalah sebagai berikut: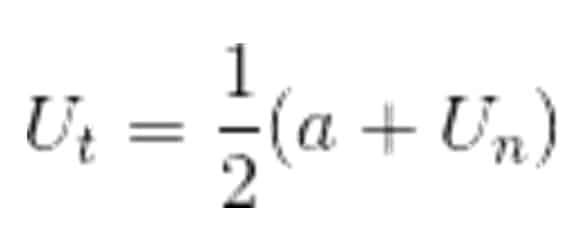
Perhatikan bahwa selisih di antara suku-sukunya selalu tetap. Barisan yang demikian itu disebut barisan aritmetika. Selisih itu disebut beda suku atau beda saja dan dilambangkan dengan c.
Barisan (l) mempunyai beda, b = 4. Barisan ini disebut barisan aritmetika naik karena nilai suku-sukunya makin besar.
Barisan (2) mempunyai beda, b = -5. Barisan ini disebut barisan aritmetika turun karena nilai suku-sukunya makin kecil.
Suatu barisan U1, U2, U3,….disebut barisan aritmetika jika selisih dua suku yang berurutan adalah tetap. Nilai Untuk menentukan suku ke-n dari barisan aritmetika. perhatikan kembali contoh barisan (l).
3, 7, 11, 15, 19, …Misalkan U1, U2, U3 , …. adalah barisan aritmetika tersebut maka
U1 = 3 =+ 4 (0)
U2 = 7 = 3 + 4 = 3 + 4 (1)
U3 = 11 = 3 + 4 + 4 = 3 + 4 (2)
….
Un = 3 + 4(n-1)
Secara umum, jika suku pertama (U1) = a dan beda suku yang berurutan adalah b maka dari rumus Un = 3 + 4(n – 1) diperoleh 3 adalah a dan 4 adalah b. Oleh sebab itu, suku ke-n dapat dirumuskan
Un = a + b(n-1)
Barisan aritmetika yang mempunyai beda positif disebut barisan aritmetika naik, sedangkan jika bedanya negatif disebut barisan aritmetika turun.
U1, U2, U3, …….Un-1, Un disebut barisan aritmatika, jika
U2 – U1 = U3 – U2 = …. = Un – Un-1 = konstanta
Un = a + (n-1)b = bn + (a-b) → Fungsi linier dalam n
Contoh Barisan Aritmatika :
Tentukanlah suku ke 15 barisan 2, 6, 10, 14, …Jawab:
n = 15
b = 6-2 = 10 – 6 = 4
U1 = a = 2
Un = a + (n-1) b
U15 = 2 + (15-1)4
= 2 + 14.4
= 2 + 56 = 58
Diketahui barisan aritmetika 3, 8, 13, …
- Tentukan suku ke-10 dan rumus suku ke-n barisan tersebut!
- Suku keberapakah yang nilainya 198 ?
- Dari barisan aritmetika 3, 8, 13, … diperoleh suku pertama a = 3 dan beda b = 8 – 3 = 5.
Un = a + (n – 1)b
U10 = 3 + (10 – 1)5
= 3 + 9 x 5
= 3 + 45
= 48
Un = a + (n – 1)b
= 3 + (n – 1)5
= 3 + 5n – 5
= 5n – 2
- Misalkan Un = 198, maka berlaku :
Un = 198Jadi 198 adalah suku ke- 40
5n – 2 = 198
5n = 200
n = 40
Deret Aritmatika
Deret Aritmatika adalah penjumlahan dari suku-suku pada barisan aritmatika.Rumus Deret Aritmatika
Bentuk umum deret aritmatika :a + (a + b) + (a+2b) + (a+3b) + … + (a+(n-1)b )
Jumlah suku hingga suku ke n pada barisan aritmatika dirumuskan dengan:
Sn = (2a + (n-1) b ) atau Sn = ( a + Un )
Seperti telah dibahas sebelumnya, deret adalah bentuk penjumlahan dari suku-suku pada sebuah barisan. Jika U1, U2, U3, … barisan aritmetika. U1, U2, U3, … adalah deret aritmetika.
Untuk mendapatkan jumlah n suku pertama dari deret aritmetika, perhatikan kembali deret yang dihasilkan barisan (l ).
3 +7 + 1l + 15 + 19 + …
Jika jumlah n suku pertama dinotasikan dengan.Sn maka S dari deret di atas adalah :
Perhatikan jumlah 5 suku pertama, S yang diperoleh. Angka 3 pada perhitungan tersebut berasal dari suku pertama, sedangkan l9 adalah suku ke-5. Oleh karena itu, jumlah suku ke-n adalah
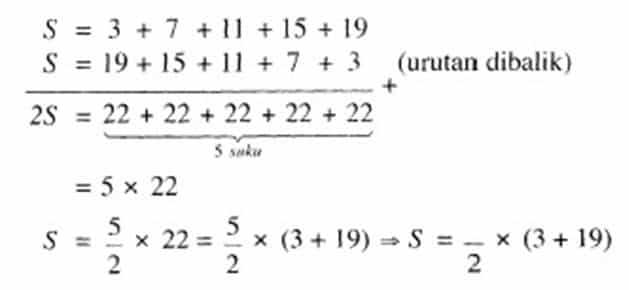
Sisipan pada Barisan Aritmatika
Apabila antara dua suku barisan aritmatika disisipkan k buah bilangan (suku baru) sehingga membentuk barisan aritmatika baru, maka:Beda barisan aritmatika setelah disispkan k buah suku akan berubah dan dirumuskan:

Keterangan:
b’ = beda barisan aritmatika setelah disisipkan k buah suku
n’ = banyak suku barisan aritmatika baru
n = banyak suku barisan aritmatika lama
k = banyak suku yang disisipkan
Sn’ = jumlah n suku pertama setelah disisipkan k buah suku
Contoh Sisipan Barisan Aritmatika
Antara bilangan 20 dan 116 disisipkan 11 bilangan sehingga bersama kedua bilangan semula terjadi deret hitung. Maka jumlah deret hitung yang terjadi adalah …Penyelesaian:
Diketahui: deret aritmatika mula-mula: 20 + 116
a = 20Jadi, jumlah deret aritmatika setelah sisipan adalah 884
Un = 116
n = 2
k = 11 bilangan
banyaknya suku baru : n’ = n + (n-1) k
= 2 + (2-1) 11 = 2 + 11 = 13
Contoh Soal Deret Aritmatika
Suatu deret aritmatika 5, 15, 25, 35, …Berapakah jumlah 10 suku pertama dari deret aritmatika tersebut?
Jawab:
n = 10
U1 = a = 5
b = 15 – 5 = 25 – 15 = 10
Sn = (2a + (n-1) b )
S10 = ( 2. 5 + (10 -1) 10)
= 5 ( 10 + 9.10)
= 5 . 100 = 500
- Jumlah suku yang pertama dari barisan 20 + 15 + 10 +…… adalah …..
b). -250
c). -75
d). -115
c). -250
Penyelesaian :
a = 20Jawaban : A
b = U2-U1
= 15-20
= -5
Sn = n (a + Un)
Un = a + (n – 1) b
U20 = 20 + (20-1)(-5)
= 20 + (19) (-5)
= 20 – 95
= – 75
S20 = . 20 (20 + (-75))
= 10 (-55)
S20 = – 550
2. Jumlah 10 suku pertama dari deret aritmatika : 3 + 5 + 7 + 9 + ….. adalah …..
a). 105
b). 120
c). 150
d). 155
e). 165
Penyelesaian :
a = 3Jawaban : B
b = U3 – U2 – 1
= U3 – U2
= 7 – 5
= 2
Sn = n (2a + (n-1)b)
= 10 (2 (5) + (10-1)2)
= 5 (6+9) 2
= 120
- Jika jumlah tak hingga dari deret geometri adalah 6 dan rasionya – , maka suku pertamanya adalah …..
b). 3
c). 8
d). 10
e). 12
Penyelesaian :
S =Jawaban : D
6 =
6 =
6 =
6 =
6 =
6 x a => 6 x 5 = = 10
- Jumlah tak hingga deret geometri adalah 6 + 2 + + adalah …..
b). 6
c). 9
d). 10
e). 18
S =Jawaban : C
a = 6
r = = =
S2 = = = 6
S2 = 6 x = = 9
- Diketahui barisan aritmatikan dengan U4 = 11 dan U8 = 23. Suku ke 15 dari suku barisan aritmatika itu adalah …..
b). 44
c). 49
d). -40
e). -44
Penyelesaian :
Un = a + (n-1)bEliminasi a + 3b = 11
= a + (4-1)b = 11
= a + 36 = 11
U8 = a + (8-1)b = 23
= a + 7b = 23
a + 7b = 23
-4b = -12
b = = 3
Substansi a + 3b = 11
a + 3 (3) = 11
a + 9 = 11
a = 11 – 9 = 2
U15Jawaban : B
Un = a + (n-1) b
U15 = 2 + (15-1) 3
= 2 + (14 x 3) = 44
- Dari suatu barisan aritmatika diketahui U2 = 7 dan U6 = 19. Suku ke 8 dari barisan aritmatika tersebut adalah …..
b). 26
c). 28
d). 31
e). 34
Penyelesaian :
Un = a + (n-1) bEliminasi :
U2 = a + (2-1) b = 7
= a + 1b = 7
U6 = a + (6-1)b = 19
= a + 5b = 19
a + 1 b = 7Subtitusi :
a + 5b = 19
-4b = -12
b = – = 3
b = 3Jawaban : A
a + 1 b = 7
a + 1 (3) = 7
a + 3 = 7
a = 7 -3 = 4
U8
Un = a + (n-1) b
U8 = 4 + (8-1) 3
= 4 + (7 . 3)
= 25
- Dari suatu barisan aritmatika diketahui U10 = 41 dan U5 = 21. U20 barisan tersebut adalah …..
b). 73
c). 77
d). 81
e). 83
Penyelesaian :
Un = a + (n-1) beliminasi :
U10 = a + (10-1)b = 41
U5 = a + (5-1)b = 21
a + 4b = 21
a + 9b = 41subtitusi :
a + 4b = 21
5b = 20
b = = 4
b = 4Jawabannya : d).
a + 9b = 41
5 +a + (9.4) = 41
a + 36 = 41
a = 41- 36
= 5
U20
Un = a + (n-1)b
U20 = a + (n-1) b
U20 = 5 + (20+1) 4
= 5 + (19.4)
= 5 + 76
= 81
- Gaji seorang karyawan setiap bulan dinaikan sebesar Rp 5.000,00jika gaji pertama gajian tersebut Rp. 100.000 …..
b). Rp. 1.255.000
c). Rp. 260.000.000
d). Rp. 1.530.000
Penyelesaian :
Sn = n (2a + (n-1) bJawabannya : d). 1.530.000
12 (2 . 100.000) +(12-1)5000
= 6 (200.000+55.000)
= 6 (225.000) = 1.530.000
- Sebuah
perusahaan mempunyai peluang untuk menjual hasil pproduksinya0,65 jika
di produksi 2.500.000unit brang, maka diperkiraan banyak hasil produksi
yang tidak terjual adalah …..
b). 875.000 unit
c). 1.125.000 unit
d). 1.375.000 unit
e). 1.625.000 unit
Penyelesaian :
. 2.500.000= 1.625.000Jawaban : B
2.500.000 – 1.625.000 = 875.000 unit
Hasil produk yang terbaik terjual adalah
- Suatu
perusahaan pada tahun pertama memproduksi 5000 unit barang, pada
tahun-tahun berikutnyaproduksinya turun secara tetap80 unit per tahun.
Pada tahun keberapa perusahaan tersebut memproduksi 3000 unit barang?
b). 25
c). 26
d). 27
e). 28
Penyelesaian :
Un = a + (n-1) bJawaban : C
3000 = 5000 + (n-1) (-80)
3000 = 5000 + (80n) + (80)
80n = 5000 – 3000 + 80
80n = 2000 + 80
80n = 2080
n = 2080 : 80 = 26
- Seorang
pemilik kebun memetik jeruknya setiap hari,dan mencatat banyaknya jeruk
yang dipetik. Ternyata banyaknya jeruk yang dipetik pada hari ke-n
memenuhi rumus Un= 50 + 25n. Jumlah jeruk yang telah dipetik selama 10
hari yang pertama adalah …..
b).1950
c).1900
d).1875
e).1825
Penyelesaian :
Sn = n (2a +(n-1)b)Jawaban : D
S10 = 10 (2.75+(10-1)25)
S10 = 5 (150+(9.25)
S10 = 5 (150+225)
S10 = 5 (375)
S10 = 1875 buah
- Dua
piluh pekerja mendapat upah harian dengan hasil pekerjaannya sebagai
berikut : pekerja 1 mendapat Rp.12.000, pekerja 2 mendapat Rp.12.500,
pekerja 3 mendapat Rp.13.000 dan seterusnya hingga upah tersebut
membentuk deret aritmatika. Jumlah upah satu hati yang harus disiapkan
oleh pemberi upah adalah …..
b).Rp. 340.000
c).Rp. 335.000
d).Rp. 220.000
e).Rp. 700.000
Penyelesaian :
Sn = n (2a + (n-1)b)Jawabannya : C
S20 =
20 (2.12000+(20-1)500)
= 20 (24000+19)500)
= 10 (24000+9500)
= 10 (33.500)
= 335.000
- Diketahui Barisan geometri dengan suku pertama 2 dan suku ke 5 = 640,maka rasionya adalah …..
b).8
c).1
d).4
Penyelesaian :
a = 2Jawaban : D
Un = a.r n-1
640 = 2 . r s-1
= r4
256 = r4
R4 = 256
R = 4
- Jika suku pertama suatu barisan geometri = 16 dan suku ketiga = 36, maka besar suku kelima adalah …..
b).-52
c).-46
d).46
e).81
Penyelesaian :
a = 16Jawaban : E
U3 = 36
Un = a r n-1
U3 = 16.r3-1
36 = 16.r2
= r2
R2 =
r =
r =
r =
U5 = 16 ( )r-1
= 16 ( )4
= 16 .
= 81
- Seseorang
berjalan kaki dengan kecepatan 8km/jam pada jam pertama. Kemudian pada
jam keduakecepatan menjadi setengahnya dari jam pertama,demikian
seterusnya. Jarak terjauh yang ditempuh orang tersebut adalah …..
b).8
c).12
d).14
e).16
Penyelesaian :
U1 = 8Jawaban : E
U2 = 4
r = = =
S2 =
=
= x
= 16
Contoh 2.1
- 1, 2, 3,… merupakan barisan aritmatika dengan beda, b = 1.
- 1, 3, 5, … merupakan barisan aritmatika dengan beda, b = 2.
- 1, -1, 1, -1,…. bukan barisan aritmatika sebab
- Diketahui barisan aritmatika dengan unsur ke 2 adalah 10 dan beda = 2.
Penyelesaian:
Karena b = Un – Un-1 = 2, maka U2 – U1 = 2. Jadi U1 = U2 – 2 = 10 – 2 = 8.
Secara sama diperoleh U3 – U2 = 2 = b. Jadi U3 = U2 + b = 10 + 2 = 12, dan
U4 = U3 + b = 12 + 2 = 14.
Menurunkan Rumus Unsur ke n Barisan Aritmatika
Jika U1 = a, U2, U3,…, Un,… merupakan barisan aritmatika, maka unsurke n dari barisan itu dapat diturunkan dengan cara berikut.
U1 = aJadi rumus umum unsur ke n suatu barisan aritmatika dengan unsur
U2 = a + b
U3 = U2 + b = (a + b) + b = a + 2b
U4 = U3 + b = (a + 2b) + b = a + 3b
U5 = U4 + b = (a + 3b) + b = a + 4b
?
Un = a + (n-1)b
pertama a dan beda b adalah:
Un = a + (n-1)bContoh 2.2
Diketahui barisan aritmatika dengan unsur ke 2 adalah 10 dan beda = 2.
Tentukan unsur ke 7 barisan itu.
Penyelesaian:
Diketahui U2 = 10, b = 2. Dengan menggunakan rumus Un = a + (n-1)b,
diperoleh
U2 = a + (2-1)bJadi unsur ke 7 dari barisan adalah 20.
U2 = a + b
a = U2 – b
= 10 – 2
= 8.
U7 = a + (7-1) b
= a + 6 b
= 8 + 6 (2)
= 8 + 12
= 20.
Contoh 2.3
Mulai tahun 2000, Pak Arman mempunyai kebun tebu. Penghasilan kebun
tebu Pak Arman pada akhir tahun 2000 adalah Rp 6.000.000,-. Mulai tahun
2001, Pak Arman memupuk kebun tebunya dengan pupuk kandang. Pak
Arman memperkirakan bahwa setiap akhir tahun, penghasilan kebun tebunya
naik Rp 500.000,-. Berapa perkiraan penghasilan kebun tebu Pak Arman pada
akhir tahun 2005?
Penyelesaian:
Misalkan:
a = penghasilan kebun tebu Pak Arman pada akhir tahun 2000.
b = perkiraan kenaikan penghasilan kebun tebu Pak Arman setiap akhir tahun.
P2005 = perkiraan penghasilan kebun Pak Arman pada akhir tahu 2005.
Jadi a = Rp 6.000.000,-, b = Rp 500.000,-, dan P2005 akan dicari.
Karena perkiraan kenaikan penghasilan kebun tebu Pak Arman setiap
akhir tahun adalah tetap, maka untuk menentukan penghasilan kebun Pak
Arman pada akhir tahun 2005, kita dapat menerapkan rumus unsur ke n dari
barisan aritmatika dengan
U1 = a = a = Rp 6.000.000,-, b = Rp 500.000.Jadi perkiraan penghasilan kebun tebu Pak Arman pada akhir tahun 2005
P2005 = U6 = a + 5b
= 6.000.000 + 5(500.000)
= 6.000.000 + 2.500.000
= 8.500.000.
adalah Rp 8.500.000,-
Dengan adanya deret aritmatika, kita dapat membentuk barisan yang
terkait dengan deret tersebut. Barisan demikian disebut barisan aritmatika.
Contoh 2.4
Tentukan jumlah 25 suku pertama deret 3 + 6 + 9 +….
Penyelesaian:
Deret 3 + 6 + 9 +…. adalah deret aritmatika dengan a = 3 dan b = 3. Oleh
karena itu dengan menggunakan rumus Sn =
1Jadi jumlah 25 suku pertama dari deret 3 + 6 + 9 +…. adalah 975.
2
n[2a + (n -1)b] diperoleh:
S25 =
1
2
(25) [2(3) + (25 -1)(3)]
=
25
2
[6 + 24(3)]
=
25
2
(6 + 72)
= 25 (39)
= 975.
Contoh 2.5
Tentukan jumlah semua bilangan ganjil antara 50 dan 100.
Penyelesaian:
Diketahui a = 51, b = 2, dan Un = 99.
Untuk mencari jumlah semua bilangan ganjil di antara 50 dan 100, pertamatama
kita cari dulu banyaknya bilangan ganjil di antara 50 dan 100, yaitu n
dengan menggunakan rumus:
Un = a + (n – 1) bSelanjutnya dengan rumus jumlah n suku pertama suatu barisan aritmatika,
99 = 51 + (n – 1)(2)
99 = 51 + 2n – 2
99 = 49 + 2n
2n = 99 – 49
n = 25.
Sn =Jadi jumlah semua bilangan ganjil antara 50 dan 100 adalah 1.875.
1
2
n[2a + (n -1)b]
diperoleh:
S25 =
1
2
(25)[2(51) + (25 -1)(2)]
= 25(51 + 24)
= 25(75)
= 1.875.

Komentar
Posting Komentar